扫码查看原文、MGE Advances期刊网址

摘要

材料的实际应用需要多个性能的同时优化，然而不同性能之间大多存在着竞争关系，一个性能的提升会以另一个性能的降低为代价，因此多目标性能的材料设计是一项复杂的任务。而多目标优化方法在多个领域已被证明是同时优化多个不同性能的有效手段。本文主要关注多目标优化方法在材料科学领域的应用，分别讨论了不同方法在材料设计与开发上的应用，最后总结并展望了多目标优化方法在材料科学上的应用前景。

文章重点内容介绍

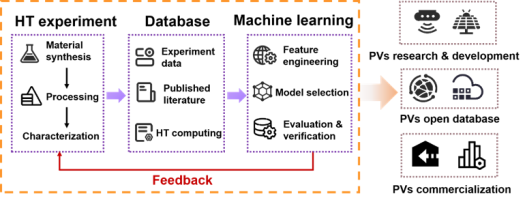
新材料的开发受限于庞大的成分组成空间，传统试错法会导致材料研发成本居高不下。机器学习方法的出现大大加快了材料研发的速度。本文的主要关注点将放在多目标贝叶斯优化等方法在材料科学和工程中的应用上，讨论了多目标优化方法如何借助机器学习等计算工具在材料设计和性能提升上发挥作用。文章第2节和第3节介绍了多目标优化的基本定义和常见方法。第4节讨论了不同的多目标优化方法在不同材料问题上的应用。最后的第5节中，我们讨论了多目标优化方法材料科学中需要进一步研究的开放性问题。

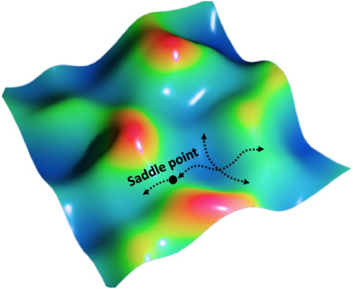
针对多目标问题，求解的目标与单目标问题不同。因为目标之间的矛盾关系，多目标优化（MOO）问题的最优解通常表示为一组权衡的解，即帕累托解集或帕累托前沿。帕累托解在搜索空间中是最优的，也就是意味着在所有目标上都没有比这些解更好性能的解，如图1所示。因此，多目标优化的主要任务是寻找特定问题的帕累托解集，将帕累托解集推进到尽可能接近目标的位置。

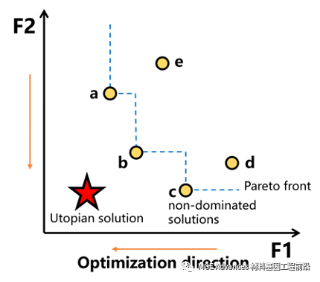
图1 帕累托面示意图

多目标优化的方法主要有三种：标量化、多目标进化算法、多目标贝叶斯优化。

标量化方法是多目标优化的常用手段，其核心思想是将多个目标按照一定的方式，比如加权求和，组合成一个新目标，根据新得到的目标进行优化和选择。

多目标进化算法是基于生物进化的思想，通过种群的选择、交叉、变异等操作，不断迭代实现优化。非支配遗传算法NSGAII是常用的多目标优化算法。该算法在遗传算法的基础上，将种群中的个体按照目标之间的非支配关系进行分层，其中第一层就是帕累托面，依此类推，直到所有的个体都有归属的层。在选择后代的时候，优先保留层数更低的个体；同一层内的个体根据计算的拥挤度从大到小进行保留。

多目标贝叶斯优化方法是将单目标贝叶斯优化方法拓展到多目标优化问题上，同时也继承了贝叶斯优化中的效能函数的概念，一方面可以基于单目标的效能函数进行优化，也可以利用基于帕累托面设计的多目标的效能函数实现迭代优化。期望超体积提升是十分重要的多目标效能函数。相比单目标优化中的目标性能直接进行比较，多目标问题将在更高维的目标性能空间内进行比较。超体积(Hypervolume)定义的是帕累托面与预先设定的参考点之间围成的空间大小，在二维空间内表现为面积。添加候选点之后超体积的增加就称为超体积提升(Hypervolume improvement)，而贝叶斯优化方法能够得到该点性能的预测值与不确定性，根据期望提升的思想，将超体积融入进去，计算得到期望超体积提升(Expected hypervolume improvement)。

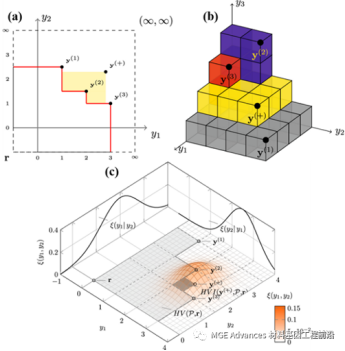
图2 期望超体积提升的示意图Copyright 2019, Springer Nature.

在材料的设计与开发中，多目标优化方法是必不可少的手段，主要有以下几种常见方法：比层次化筛选、单目标化方法、基于帕累托前沿推进的遗传算法和多目标贝叶斯优化方法等。

层次化筛选主要依赖于材料性能的预测结果，根据领域知识，依照不同的性能需求对目标材料进行逐步筛选，最终获得具有优化性能的材料。单目标化方法将多个目标映射到一个目标上，通过对性能的重新组合，结合机器学习模型对性能的预测，基于这个新目标对新材料进行选择。多目标遗传算法在选择后代时，利用机器学习模型预测材料性能，并以此作为依据搜索帕累托面，通过迭代不断优化帕累托面。多目标贝叶斯优化方法基于主动学习的理念，通过构建模型，对性能进行预测，并且选择实验进行迭代优化。既可以设计针对目标性能点的效能函数进行性能优化，也可以从推进帕累托面的角度，实现帕累托面的提升进而发现具有优化性能的材料。

图3 多目标优化方法实现材料性能提升Copyright 2020, Elsevier.

综上所述，将机器学习方法和多目标优化方法相结合有助于优化材料多个性能的同步优化，而考虑不确定性的多目标优化方法也有望成为进一步提高材料性能多目标优化效果的有效手段。

通讯作者

薛德祯，于2012年获西安交通大学材料科学与工程专业博士学位，曾在美国洛斯阿拉莫斯国家实验室从事博士后工作，现为西安交通大学教授。主要研究方向为铁性智能材料和材料信息学，以机器学习辅助实现铁性材料的高性能化，致力于材料学与信息学的交叉融合。提出的材料自适应设计方法，能够有效减少实验次数，仅通过少量实验反馈迭代，成功开发出多种新型功能材料，相关方法被MRS Bulletin 专题推介指出，“为新材料的设计开发提供了最好的统计学方法”。

第一作者

史博枫，西安交通大学材料科学与工程学院博士生，研究方向为材料信息学。